قوانین کپلر و اثبات آنها
آشنایی :
کیهان شناسی همواره یک منبع الهام بخش برای علم بوده است . احتمالا بسیاری از حرکت های انقلابی در علم از ستاره شناسی شروع شده است . تمدن های قدیم نیز به قوانینی که بر حرکت اجرام آسمانی حکومت می کند پی برده بودند و می دانستند که این کائنات به خودی خود و بدون ترتیب جابجا نمی شوند . تئوری وجود نیرو به بطلیموس بر می گردد او اینطور تصور می کرد تمامی اجرام در آسمان به دور زمین می چرخند و حرکت آنها یک حرکت دوار است . بعضی از ستارگان ( که بعدها معلوم گشت آنها سیاره بوده اند ) حرکاتی نامنظم داشتند و به پارامتر های زیادی جهت تبیین حرکت آنها نیاز بود . این تئوری تخمین های تقریبا دقیقی به دست می داد اما بدست آوردن یک پارامتر آن کاری سخت و طاقت فرسا بود .
با استفاده از اطلاعات جمع آوری شده توسط تیکو براهه 3 قانون زیر را نوشت Johanns Keplerدر قرن 17
1 : هر سیاره در مداری بیضی به دور خورشید که در یکی از کانون های بیضی قرار دارد می چرخد .
2 : شعاع اتصال یا خط واصل خورشید و سیاره مساحت های مساوی را در زمان های مساوی طی
می کند
![]() یا به صورت ریاضی :
یا به صورت ریاضی :
3 : مربع دوره ی تناوب مداری سیاره متناسب است با مکعب نصف قطر بزرگ مدار
![]() یا
یا ![]() یا به صورت ریاضی :
یا به صورت ریاضی :
و یکی نصف قطر بزرگ بیضیe برای هر سیاره ما به 2 پارامتر بیشتر نیاز نداریم : یکی دوری از مرکز یا
سپس حرکت توسط این 3 قانون توصیف می شود برای مثال قانون دوم سرعت زاویه ای را در هر نقطه از مدار به ما می دهد و می توان دریافت که هر چه سیاره به خورشید بیشتر نزدیک می شود سرعت آن افزایش می یابد و در نهایت قانون سوم سرعت خطی سیاره را به ما می دهد .
قوانین حرکت و Philosophiae Naturalis Principia Mathematicaدر سال 1687 نیوتن در شاهکار خود
گرانش خود را برای بدست آوردن قوانین 3 گانه ی کپلر به کار برد جالب است بدانید این قوانین به هر جسمی که تحت تاثیر نیروی گرانش دور چیزی می چرخد می توان اعمال کرد .
برای اثبات قانون اول نیوتن می بایست ابتدا معادله ی بیضی را در دستگاه مختصات قطبی داشته باشیم
پس باید معادله ی بیضی در دستگاه دکارتی را داشته باشیم .
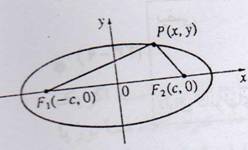
![]()
همان نصف قطر بزرگ بیضی است اثبات رابطه ی بالا :a
ها بسته شده است بوجود می آورند پس طول نخ Fمی دانیم که بیضی را توسط یک نخ که 2 سر آن به
قرار می دهیم و بیضی را
می کشیم هنگامی که نوک pمی باشد نوک مداد را در ![]() برابر با
برابر با
می شود .2a ها را قطع کرد اندازه ی آن xمداد محور
![]()
فاصله ی یکی از کانون ها تا مرکز بیضی است .c
![]()
2 طرف را به توان 2 می رسانیم .
![]()
که به صورت زیر ساده می شود .
![]()
2 طرف را به توان 2 می رسانیم .
![]()
![]() را با عبارت
را با عبارت ![]() از 2 طرف حذف
می شود جای عبارت
از 2 طرف حذف
می شود جای عبارت ![]() را در پرانتز
اثر می دهیم عبارت
را در پرانتز
اثر می دهیم عبارت ![]()
فاکتور می گیریم .![]() و در سمت چپ از
و در سمت چپ از ![]() تعویض می کنیم در راست از
تعویض می کنیم در راست از
![]()
همان نصف قطر
کوچک بیضی است بوسیلهb و می دانیم
که ![]() برای راحتی فرض می کنیم
برای راحتی فرض می کنیم
قضیه ی فیثاغورس رابطه ی بالا به سادگی بدست می آید . با جایگذاری داریم .
![]()
تقسیم
می کنیم . ![]() 2 طرف را بر
2 طرف را بر
![]()
رابطه ی بالا معادله ی بیضی در دستگاه مختصات دکارتی است .
حال می خواهیم معادله ی بیضی را در دستگاه مختصات قطبی پیدا کنیم .
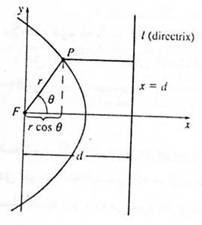
![]()
![]()
![]()
اینگونه است .e را برون مرکزی بیضی می نامند و با رابطه ی بالا می شناسند . در مختصات قطبی e
![]() =e
=e
در جریان محاسبه می بینیم که این رابطه درست است . پس داریم .
![]()
![]() و
و ![]() می دانیم که
می دانیم که
2 طرف را مربع می کنیم عبارات بالا را جایگزین می کنیم .
![]()
فاکتور ![]() را به سمت چپ
می بریم و از
را به سمت چپ
می بریم و از ![]() و
و ![]() را در پرانتز
اثر می دهیم و عبارات
را در پرانتز
اثر می دهیم و عبارات ![]()
می گیریم .
![]()
را اضافه می کنیم . این عمل را ![]() تقسیم می کنیم . به 2 طرف عبارت
تقسیم می کنیم . به 2 طرف عبارت ![]() 2 طرف را بر
عبارت
2 طرف را بر
عبارت
انجام دادیم تا عبارت زیر بدست آید .
![]()
اگر عبارات زیر را داشته باشیم :
![]() ,
, ![]() ,
, ![]()
عبارت به صورت زیر در می آید :
![]()
را می نویسیمe درست است eکه معادله ی یک بیضی است حال برای آنکه بدانیم تعریف ما از
![]()
![]()
![]()
![]()
![]()
![]()
![]()
همان چیزی که انتظار آن را داشتیم پس معادله ی بیضی در دستگاه مختصات قطبی چنین است :
![]()
اثبات قوانین کپلر :
قانون اول :
همانطور که قبلا نیز گفته شد قانون اول بیان می کند که هر جسمی که تحت تاثیر نیروی گرانش جسم دیگری باشد در مداری بیضوی دور آن می چرخد .
2 اثبات برای این قانون اینجا ذکر می کنیم .
اثبات 1 :
برای اثبات این که سیاره بیضوی می چرخد ابتدا باید ثابت کنیم که در یک صفحه می چرخد لذا داریم
![]() قانون دوم نیوتن :
قانون دوم نیوتن :
![]() قانون گرانش
نیوتن :
قانون گرانش
نیوتن :
ابتدا باید عرض کنم حروفی که کج نوشته شده اند نشاندهنده ی اندازه اند و حروفی که به صورت معمولی نوشته شده اند نشاندهنده ی بردار اند .
جرم سیارات به ترتیب جرم دور زننده و جرم ثابت می باشندM و m نیروی گرانشی روی سیاره ، F
می باشد .r بردار
یکه در سوی ![]() و
و ![]() ثابت گرانش ، G
ثابت گرانش ، G
های 2 قانون را برابر با هم قرار می دهیم .F
![]()
ها از طرفین ساده می شوند .m
![]()
است پس موازیند و داریم .r ضریبی از بردار aو بنابراین می فهمیم که بردار
![]()
![]()
![]()
بردار سرعت است بنابر این داریم :v
![]()
بر 2 بردارh نتیجه می شود که بردار ثابت ![]() یک بردار ثابت است و حال اگر
فرض کنیم که hکه در آن
یک بردار ثابت است و حال اگر
فرض کنیم که hکه در آن
هر دو در یک صفحه اند .v و بردار r عمود است پس بردار v و r
می دانیم که بردار سرعت همواره بر مسیر حرکت مماس می باشد پس مدار بر یک صفحه قرار دارد .
شروع می کنیم به اثبات قانون اول کپلر داریم :hاز بردار ثابت
![]()
![]()
![]()
پس بنابر این داریم :
![]()
قضیه ای است در مورد ضرب خارجی که بیان می کند که :
![]()
جای اثبات این قضیه نیست آن را می پذیریم و ادامه می دهیم .
![]() داشته باشد آنگاه بردار مکان بر بردار مماس آن عمود است پس
در در اینجا
داشته باشد آنگاه بردار مکان بر بردار مماس آن عمود است پس
در در اینجا
![]()
![]()
با انتگرال گیری از 2 طرف داریم :
![]()
یک بردار ثابت است .cکه در آن
باشد مناسب h در سوی بردار Kدر اینجا انتخاب محور های مختصات به طوری که بردار پایه استاندارد
عمودند برابری بالا h بر u و ![]() حرکت می
کند . چون هر دوی xyاست . در این صورت سیاره در صفحه
حرکت می
کند . چون هر دوی xyاست . در این صورت سیاره در صفحه
را طوری انتخاب کنیم که y و محور x قرار دارد یعنی می توانیم محور xy در صفحه cنشان می دهد که
قرار گیرد .c در سوی iهمان طور که در شکل نشان داده شده است بردار
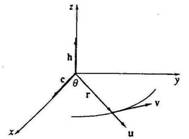
مختصات قطبی سیاره می باشند از
برابری بالا داریم .![]() باشد آنگاه v و c زاویه ی بین
باشد آنگاه v و c زاویه ی بین ![]() اگر
اگر
![]()
![]()
![]()
تقسیم
کنیم داریم![]() در سمت راست معادله فاکتور
بگیریم و 2 جمله را بر عبارت rاگر از
در سمت راست معادله فاکتور
بگیریم و 2 جمله را بر عبارت rاگر از
![]()
![]() که در آن
که در آن
در جای دیگر داریم
![]()
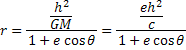
داریم ![]() و اگر داشته باشیم
و اگر داشته باشیم
![]()
و این همان معادله ی قطبی بیضی است .
اثبات 2 :
اثبات دوم قانون اول کپلر از طریق انرژی و تکانه ی زاویه ای سیاره محاسبه می شود . برای این اثبات ابتدا باید مفاهیمی را مقدمه بنویسیم :
تبدیل دستگاه مختصات دکارتی به قطبی :
![]()
از هر 2 و از هر 2 طرف آنها دیفرانسیل می گیریم .
![]()
![]()
![]()
فاکتور
می گیریم .![]() و
و ![]() از بین
می رود از
از بین
می رود از ![]() عبارت
عبارت
![]()
![]()
انرژی :
انرژی را ما همیشه به صورت جمع انرژی جنبشی و پتانسیل داشتیم حال نیز این کار را می کنیم . اما ما هر 2 برابر با 1 شوند .GM و mبرای راحتی کار واحد دستگاه را طوری انتخاب می کنیم تا
![]()
![]()
![]()
همان نیروی گرانش است . پس :Fرابطه ی
![]()
ساده می شود به صورت زیر :
![]()
![]()
![]()
تکانه ی زاویه ای :
![]()
![]()
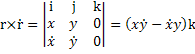
![]()
![]()
![]()
![]()
را قرار می دهیم .![]() عبارت
عبارت ![]() را در پرانتز اثر می دهیم
و به جای
را در پرانتز اثر می دهیم
و به جای ![]()
![]()
را به سمت چپ
می بریم و تمام معادله را در 2 ضرب می کنیم داریم :![]() عبارت
عبارت
![]()
![]()
![]()
2 عبارت بالا را بر هم تقسیم می کنیم .
![]()
از 2 طرف دیفرانسیل می گیریم :
![]()
تقسیم
می کنیم .![]() معادله را بر
معادله را بر
![]()
یک تغییر متغیر می تواند به ما کمک کند
![]()
می
گیریم .![]() از 2 طرف دیفرانسیل نسبت به
از 2 طرف دیفرانسیل نسبت به
![]()
یک بار دیگر دیفرانسیل می گیریم .
![]()
با جایگذاری داریم :
![]()
ساده می کنیم :
![]()
به سمت چپ می بریم .u
![]()
حال به یاد بیاورید این روابط را :
![]()
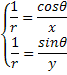
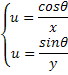
دیفرانسیل
می گیریم .![]() از هر 2 و از هر 2 طرف نسبت به
از هر 2 و از هر 2 طرف نسبت به
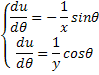
دیفرانسیل می گیریم .![]() از هر 2 و از هر 2 طرف نسبت به
از هر 2 و از هر 2 طرف نسبت به
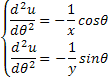
ضریبی از سینوس و کسینوس است .u حال دیدیم که مشتق دوم
پس داریم :
![]()
را قرار
می دهیم .e برون مرکزی ![]() تبدیل
می کنیم . و به جای
تبدیل
می کنیم . و به جای ![]() را به uدوباره
را به uدوباره
![]()
که مشاهده می کنیم مختصات قطبی یک بیضی را به ما می دهد .
قانون دوم :
همان طور که ذکر شد این قانون بیان می کند که سیاره مساحت های مساوی را در زمان های مساوی طی می کند .
برای اثبات ما داشتیم :
![]()
و می دانیم مساحت حاصل از یک شعاع که بیضی را جارو می کند با رابطه ی زیر داده می شود .
![]()
از 2 طرف دیفرانسیل می گیریم .
![]()
![]()
مقداری ثابت دارد . پس دیفرانسیل آن باید صفر شود .Lحال باید ثابت کنیم که
2 عبارت پایین را به خاطر بیاورید :
![]() قانون دوم نیوتن :
قانون دوم نیوتن :
![]() قانون گرانش نیوتن :
قانون گرانش نیوتن :
![]()
![]()
از 2 طرف دیفرانسیل می گیریم .
![]()
مقداری ثابت دارد پس قانون دوم ثابت می شود .Lپس
قانون سوم :
در این قانون ما می بایست رابطه ای بین مربع دوره ی تناوب سیاره دور خورشید و مکعب نصف قطر بزرگ مدار سیاره پیدا کنیم .
رابطه ی زیر را بخاطر بیاورید .
![]()
![]()
دوره را انتگرال روی بازه های زمانی گرفت .
![]()
قرار می دهیم .rمقدار ثابت شده در اثبات قانون اول بروش اول را بجای
![]()
r(max) و دورترین فاصله سیاره از خورشید را با r(min)می دانیم که اگر نزدیکترین فاصله ی سیاره را با
نشان دهیم این روابط را داریم :
![]()
![]()
![]()
اگر به 2 طرف مقدار یک را اضافه کنیم داریم .
![]()
و اگر همان رابطه ی قبلی را در منفی ضرب کنیم و مقدار یک را به آن اضافه کنیم داریم .
![]()
حال 2 رابطه ی بدست آمده را در هم ضرب می کنیم .
![]()
![]()
![]()
داریم :
![]()
2 طرف را در 2 ضرب می کنیم .
![]()
![]()
![]()
![]()
![]()
![]()
2 عبارت بالا را با هم جمع می کنیم .
![]()
![]()
این عبارت را داشتیم که :
![]()
را قرار
می دهیم .![]() عبارت
عبارت ![]() بجای
بجای
![]()
![]()
![]()
پس قانون سوم هم اثبات شد ...
نویسنده : رضا نادری
منابع :
به نام قوانین کپلر Gilbert Weinstein مقاله ای از
نوشته ی جیمز استوارتCalculus Differential & Integralکتاب
کتاب آشنایی با مکانیک اثر دانیل کلپنر